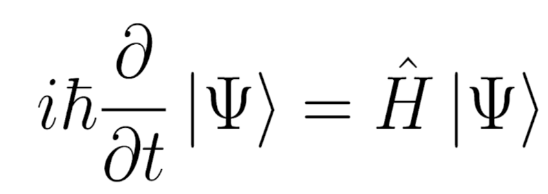The Quantum Revolution: Pivotal Advances that redefined Physics

Abdelrahim Bazina • 2025-02-18

The emergence of quantum mechanics in the early 20th century shook the groundwork of physics. A probabilistic theory that fundamentally challenged Newtonian mechanics left physicists confused by the profound implications it held.

The sequential development of quantum mechanics in the 20th century serves as proof of the progressive, collaborative nature of science. By understanding how physicists adapted to new discoveries and challenged the very framework of their study, scientists can foster a more critical, reflective community.

In the early 20th century, physics was thought to be complete. The combination of Newton’s classical mechanics, electromagnetism and thermodynamics provided a seemingly comprehensive framework for understanding the natural world.

However, this notion was disrupted when Max Planck introduced a quantum hypothesis: proposing that energy was ‘quantised’ in discrete packets, or quanta. Shortly after, Einstein would further quantum theory with his work on the ‘photoelectric effect’, introducing a paradoxical concept that would challenge the classical theory of light. The idea of wave-particle duality, that particles exhibit both wave and particle-like behaviour proved to be the explanation for phenomena like electron diffraction. This was famously demonstrated in the double slit experiment, where electrons, when not observed, created an interference pattern akin to that of classical waves. However, when measured, they appeared to behave as discrete particles.

This caught the attention of Niels Bohr, who built on the newly discovered nuclear model of the atom to introduce quantized electron energy levels to explain atomic structure. Bohr’s model suggested that electrons can only occupy certain allowed energy levels, and transitions between these levels resulted in the loss or gain of energy in the form of electromagnetic radiation. Building on Bohr’s ideas, Johannes Rydberg would formulate his ‘Rydberg equation’.

Figure 1 - Rydberg Equation

Figure 1 shows the Rydberg equation, used to calculate the wavelengths of light emitted by electrons during their transition between energy levels. The principal quantum number, ‘n’, refers to each electron shell. Wavelength, inversely proportional to the frequency, is used as a relative measure of energy, whilst the Rydberg Constant, RH, calculated experimentally, is used to relate these quantities. The equation essentially describes the difference in energy between During this period, Erwin Schrödinger devised a wave equation that provided a framework for understanding the time-evolution of quantum systems. The time dependent Schrödinger equation states that the changes that occur to a quantum system over a given time are governed by the system’s energy. Analogous to Newton’s second law, the Schrödinger equation can be solved to yield all known information about a quantum system: encapsulated in the quantum wave function. By performing certain calculations, we can discern information about the quantum system from this wavefunction. The Schrödinger equation is the most fundamental mathematical principle underlying this theory: succinctly governing quantum systems and serving as the fundamental equivalent to Newton’s second law.

Figure 2 - Time Dependent Schrödinger equation Figure 2 shows the equation in one of its simplest forms. The Hamiltonian Operator, denoted Ĥ, is the sum of the kinetic and potential energy operators acting on the system. The Hamiltonian contains all information about the system’s energy, scaling the wavefunction by an eigenvalue (a scalar) of the corresponding quantised energy.

Schrödinger’s revolutionary wave mechanics would pave the way for Werner Heisenberg’s ‘Uncertainty Principle. Schrödinger’s work introduced the quantum wavefunction, a mathematical description of the probability distribution of particles like electrons. The probabilistic nature of this description implied that the universe is inherently non-deterministic.

Heisenberg’s ‘Uncertainty Principle’, derived from the commutator of position and momentum and the Cauchy-Schwarz inequality, mathematically proved that the position and momentum of a quantum system cannot both be known simultaneously. In quantum mechanics, observables are governed by operators. When measuring these observables, fluctuations arise. At certain points, the system appears to exhibit a single value for this arbitrary quantity: this is called an eigenstate. Heisenberg’s work stressed that one cannot be in both an eigenstate of position and momentum at the same time. This principle is a direct consequence of the wave-like nature of particles described by Schrödinger’s wave function.

Arising from Schrödinger’s wave mechanics, and crucial to grasping the Uncertainty Principle, is the concept of quantum superposition. According to Schrödinger’s equation, particles such as electrons do not exist in just one definite state but can be in a superposition of multiple states simultaneously. This means an electron, for example, can occupy more than one position or energy level until it is observed or measured, at which point the wave function collapses to a single, definite state.

This idea was famously encapsulated in Schrödinger’s thought experiment, known as Schrödinger’s Cat. In this hypothetical scenario, a cat inside a sealed box could be considered both alive and dead at the same time, depending on the outcome of a quantum event. The cat only assumes a definite state-either alive or dead-once the box is opened and the system is observed.

Superposition highlights the inherently non-deterministic nature of the quantum world, a stark contrast to the certainties of classical mechanics. It serves as a cornerstone of quantum theory, challenging our understanding of reality and prompting philosophical questions about the nature of existence itself.

In quantum mechanics, nothing is certain until observed. Superposition, along with the probabilistic wave function and the Uncertainty Principle, demonstrates the fundamentally counterintuitive and mind-bending nature of quantum theory, redefining what we consider to be real.

Another key figure in the 20th-century quantum revolution, one who shared the 1933 Nobel Prize in physics with Schrödinger, was Paul Dirac, whose groundbreaking work further unified quantum mechanics with the principles of special relativity. Introduced in 1905 by Einstein, special relativity defined the speed of light as a constant, and stated that time is relative, dependent on an observer's motion.

In 1928, Dirac developed the Dirac equation, which provided a relativistic description of the electron and predicted the existence of antimatter. This theoretical prediction was later confirmed with the discovery of the positron, marking one of the first major triumphs of quantum theory in describing previously unknown particles.

Dirac’s equation also played a pivotal role in the development of Quantum Electrodynamics (QED), the quantum theory of electromagnetic interactions, which would become one of the most accurate theories in all of physics. His contributions laid the groundwork for later advancements in particle physics, such as the development of the Standard Model, further cementing the quantum revolution in the field.

As the 20th century closed, the principles of quantum mechanics began to pave the way for revolutionary technologies, most notably quantum computing. Quantum computers leverage the concept of superposition to perform calculations at speeds unattainable by classical computers. Unlike classical bits that exist in a state of 0 or 1, quantum bits, or qubits, can represent both 0 and 1 simultaneously, allowing quantum computers to process vast amounts of information concurrently.

The potential applications of quantum computing are vast, ranging from drug discovery and materials science to optimization problems and secure communications. For instance, quantum algorithms like Shor’s algorithm could theoretically break widely used cryptographic schemes, prompting a reevaluation of data security in the digital age.

Additionally, as research in quantum mechanics continues to advance, we may see further developments in quantum technologies, including quantum sensors and quantum networks, which could revolutionise fields such as telecommunications and precision measurement. These advancements not only hold the promise of solving complex problems but also challenge our foundational understanding of reality itself.

The future of quantum mechanics is poised to transform not only our technological landscape but also our philosophical perspectives on nature, knowledge, and the universe. As we continue to explore this intricate and fascinating domain, the journey of quantum mechanics from its humble beginnings to its current and future applications stands as a testament to the power of human inquiry and collaboration in the pursuit of knowledge.

The confusion faced by the scientific community in the early 20th century, and their ability to collaboratively develop a new field that disagreed with intuition, highlights the importance of sequential discovery and the impacts of nucleating abstract thinking.

References

What is Quantum Mechanics?” - Stanford Encyclopedia of Philosophy

The Uncertainty Principle” - Physics.org

Quantum Mechanics Explained” - Quantum Magazine

The Basics of Quantum Mechanics” - Live Science

Wave-Particle Duality” - Physics Central

Understanding Quantum Superposition” - Scientific American

Schrödinger’s Cat Explained” - HowStuffWorks

The Quantum World: An Overview” - Nobel Prize Education

Dirac’s Equation and the Electron” - American Physical Society

The Role of Quantum Mechanics in Chemistry” - Royal Society of Chemistry

Quantum Mechanics in Everyday Life” - Physics World