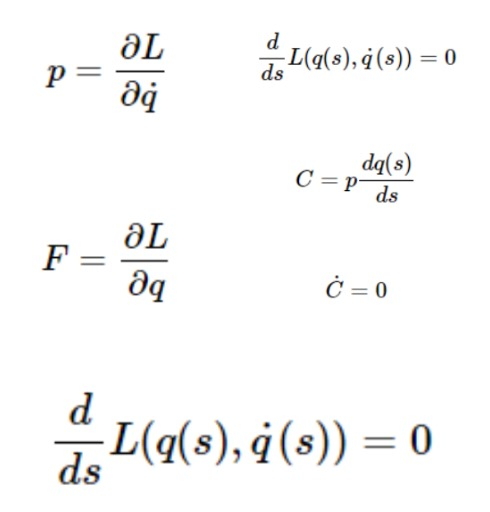NOETHER’S THEOREM AND SYMMETRIES
Manasvi Kommuri • 2024-10-17
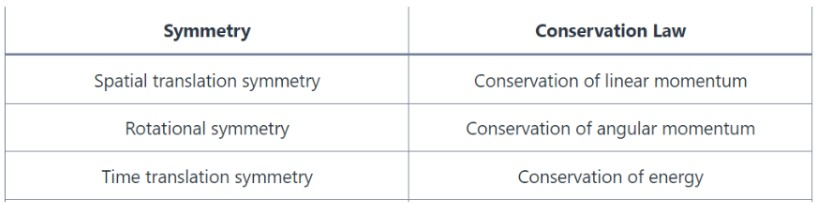
𝙄𝙣𝙨𝙩𝙞𝙩𝙪𝙩𝙚 - 𝙃𝙚𝙣𝙧𝙞𝙚𝙩𝙩𝙖 𝘽𝙖𝙧𝙣𝙚𝙩𝙩 𝙎𝙘𝙝𝙤𝙤𝙡 Noether's theorem is a remarkable result that allows mathematicians and physicists to derive conserved quantities from the symmetries of natural laws. For example, time translation symmetry leads to the conservation of energy, space translation symmetry results in the conservation of momentum, and rotational symmetry yields the conservation of angular momentum, among others.
Proven by Emmy Noether in 1915, shortly after she arrived in Göttingen, the theorem was lauded by Einstein as a work of "penetrating mathematical thinking." Today, it serves as a foundational tool in theoretical physics.
Noether’s theorem is the statement that for every continuous symmetry in a physical system, there exists a conservation law. A symmetry of a physical system, in the context of Noether’s theorem, means a transformation to the system that leaves its equations of motion unchanged.
There are many reasons as to why Noether’s Theorem is important. It tells us where fundamental conservation laws, such as conservation of momentum and energy, actually come from. Noether’s theorem also helps us find what symmetries a physical system has, given that we know a particular conservation law exists. Noether’s theorem also provides a structured way of constructing new theories of physics – in practice, it provides a guiding light for building Lagrangians for different theories, given that we want a certain conservation law to be a part of the theory. Noether’s theorem gives us a straightforward and quantitative way to identify conserved quantities in practice from the Lagrangian of a system.
In simple terms, Noether’s theorem is a general statement about the interplay between symmetries and conservation laws. This article will try to explain the proof of Noether’s Theorem in simple terms, however, Newtonian mechanics isn't sufficient to prove the theorem, instead, Lagrangian mechanics will be needed. Lagrangian mechanics are a reformulation of classical mechanics that rely on Hamilton's stationary action. However, for our purposes we do not need to understand how one would use them to solve for the dynamics of a physical system.
First, we must understand what symmetries mean in the physical sense.
In physics/applied mathematics, a symmetry of a physical system is any transformation that leaves a system physically unchanged and is mathematically defined as a transformation that only changes the Lagrangian up to a total time derivative. Examples include rotations of a system under a central force field.
The idea of symmetry in physics is a bit different than what you may intuitively picture a symmetry as (for example, a geometric object “looking” the same on both sides). When we talk about symmetries of physical systems, we always mean transformations of the system. A transformation, intuitively, is something we can do to a system to change it in some way – for example, we could move a system in space by 5 meters to the right.
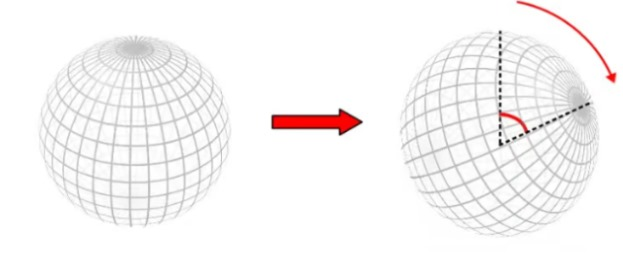
In most cases, a transformation will certainly change a physical system. However, there are special cases where the system is physically unchanged by a specific transformation and these transformations are what we call symmetries of the system. So, a symmetry in physics is really a transformation of some kind and always has to be associated with one. Perhaps the simplest example of a symmetry would be the rotation of a sphere, as shown above. A rotation is a transformation of the sphere that leaves it completely unchanged – therefore, it is a symmetry of the sphere (we call this spherical symmetry).
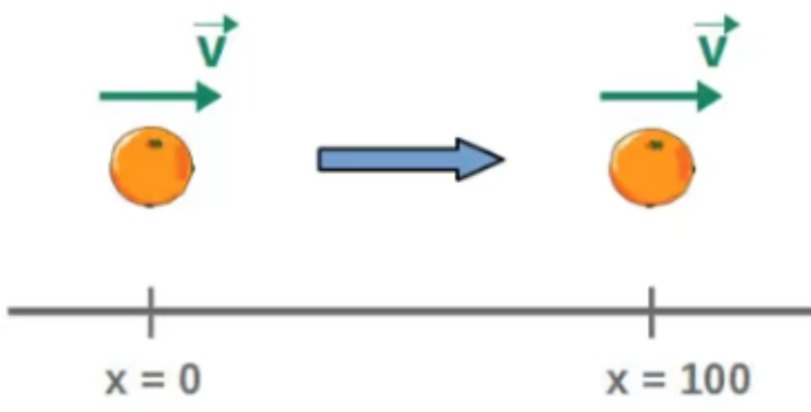
A more physically relevant example would be a spatial translation of a free particle (a particle that isn’t affected by any forces). This is a symmetry of the single-particle system, since moving the particle in space by a constant amount does not actually change the physics of the particle in any way – since it’s a free particle, its motion will be exactly the same at all points in space and it makes no difference whether we look at the particle at x=0 or at x=100. IE. The physics of a free particle remain unchanged under a spacial shift, otherwise known as spatial translation symmetry.
However, the crucial part here is that this is a free particle. If there were forces present that vary from point to point in space, then moving the particle to a different location would certainly change its motion, since there would be a different force acting on the particle at the new location – spatial translations would not be a symmetry of the system anymore. Furthermore, rotational symmetry refers to a system's physics remaining unchanged when rotated around a particular axis, and Noether’s theorem connects this to the conservation of angular momentum. Similarly, time translation symmetry means that shifting a system forward in time leaves its behavior unaffected, so the system behaves the same whether observed now or later. However, when an external force varies with time, this symmetry is broken. Noether’s theorem links time translation symmetry to the conservation of energy. The very simplified proof, as explained by John Baez is as follows:
Suppose we have a particle moving on a line, with Lagrangian L(Q, Q̇ ) where Q is its position and Q̇ = dq/dt (ie its velocity as a derivative).
The momentum of the particle and the force on it is defined to be: The equations of motion - the so-called Euler Lagrange equations, say that the rate of change of momentum equals the force. Therefore Ṗ = F Now suppose the Lagrangian L has a symmetry meaning that it doesn’t change when you apply some one-parameter family of transformations sending Q to some new position Q(S). This allows us to identify figure 2 and allows mathematicians to make the claim of what C equals to and define it as a conserved quantity. Now, we take the time derivative of our supposed conserved quantity using the product rule. We can use the equation of motion of our particle and the definition of momentum to rewrite Ṗ and P in terms of this equation. And then use the chain rule to find the right side of the equation.
Therefore C is conserved (as it equals 0) and the theorem is proved. Although this is undoubtedly an interesting result, in classical mechanics there are only three types of symmetries and so this seems like an unnecessarily large amount of machinery to build to show the conservation of the three classical quantities. The use becomes far more evident in theoretical physics. One starts with a more general version of the theorem, which allows us to consider fields instead of only particles. In many settings, it is possible to write down the Lagrangian (or Lagrangian density) of the system. We can then study this system by trying to find symmetries of it. In most cases, one will obtain a Lie group called the “gauge group” of the system. By studying the associated Lie algebra of this gauge group, one finds the conserved quantities in the system. This is a standard tool for modern physicists and it has been said that Noether’s theorem is second only to Pythagoras’ theorem in importance for modern physicists. By using this in general relativity, one unifies the conservation of momentum and energy and shows why matter seems to be conserved on a day-to-day basis even though a priori there is no corresponding symmetry. However, the theorem really shines in particle physics and quantum mechanics.
Noether's theorem stands as one of the most profound and unifying principles in theoretical physics, linking the symmetries of nature's laws to conserved quantities like energy, momentum, and angular momentum. By revealing the deep connection between mathematical symmetry and physical conservation laws, it provides a powerful framework for understanding and predicting the behavior of physical systems. This insight has not only shaped modern physics but continues to be an essential tool in advancing new theories and uncovering the underlying order of the universe. In order to study this theorem on a deeper level, prerequisite knowledge of Lagrangian and Hamiltonian mechanics, calculus of variations, group theory and field theory is needed but the aim of this article was to provide an introduction to Noether’s Theorem and symmetries in physics.
See More Posts
Copyright © 2021 Govest, Inc. All rights reserved.